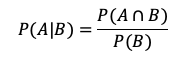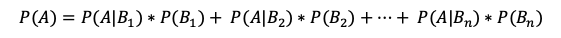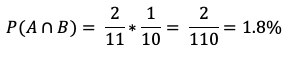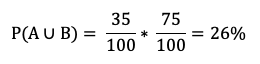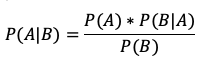3- Principios generales de probabilidades

3.8- Qué es una probabilidad condicional

La probabilidad condicional es la probabilidad de que un evento suceda dado que otro evento ya ocurrió. Si el evento en el que estamos interesados es A y el evento B es conocido, la probabilidad condicional se denota como P(A|B) es decir la probabilidad de A dado B ya ocurrió. Esta probabilidad se da cuando dos eventos son dependientes de manera que la P(A ∩ B) = P(A) * P (B). Si los eventos son independientes entonces la P(A|B) = P(A).

Donde P(A│B) representa la probabilidad de A dado que B ha ocurrido. P(A∩B) Representa la probabilidad de la intersección y P(B) Representa la probabilidad del evento B.

Solo es de interés el resultado si se cumple B y la P(B) debe ser mayor que 0. Únicamente los elementos de la intersección podrían hacer que se cumpla B, por tanto deben haber elementos en común. Ojo aquí el orden es importante, la P(A|B) no es igual que la P(B|A) (Porto y Gardey, 2019). Es importante aclarar que en la probabilidad condicional no necesariamente puede haber una relación temporal o causal entre los dos componentes, esto quiere decir que A puede producirse antes que B, después o al mismo tiempo y que A puede ser el origen de B o viceversa o no tener ningún tipo de relación.

Por ejemplo, un investigador toma una muestra de 100 fincas de una región de la costa colombiana. De esas 100 fincas 80 tienen producción ganadera y 45 tienen producción ganadera y reforestadora a la vez (doble propósito) y solo 20 son de orientación exclusivamente reforestadoras. ¿Cual será la probabilidad de encontrar una finca que tenga actividad reforestadora cuando en principio ha sido seleccionada una finca de orientación ganadera?

• Espacio muestral: 100 fincas de la costa colombiana
• P(A ∩ B)= 45/100
• P(B) = 80/100


• P(A|B)= 0.45/0.80 = 56%

3.9- Regla de la probabilidad total

La regla o teorema de la probabilidad total permite calcular la probabilidad de un evento a partir de varias probabilidades condicionadas. Por ejemplo cuando buscamos la probabilidad de encontrar un animal afectado con mastitis clínica (MC) en un conjunto de animales que tienen una característica determinada como son vacas con altos niveles de células somáticas -CCS- en la leche y su complemento que son las vacas con bajos niveles de células somáticas en leche.
Entonces para cualquier conjunto de A (probabilidad de A o seleccionar un animal afectado con MC), estaría dado por la unión de varios conjuntos mutualmente excluyentes B1, B2 ... Bn (animales con elevado número de CCS + animales con bajo número de CCS), su probabilidad es igual a la siguiente suma:

Donde P(A) es la probabilidad de que ocurra el evento A, P(A│B₁) es la probabilidad condicional de A dado que B₁ha ocurrido, P(B₁) es la probabilidad de que B₁ ocurra. P(A│B_n) es la probabilidad condicional de A dado que B_nha ocurrido. P(B_n) es la probabilidad de que B_n ocurra.

Ejemplo, en un estudio epidemiológico se encuentra que de una muestra aleatoria de 100 hatos, al realizar el conteo de células somáticas en leche, el 60% tienen niveles adecuados de CCS (≦4), mientras que el 40% restantes tiene niveles superiores a 4 por tanto muy elevados. De los hatos con adecuados niveles de CCS la prevalencia de Mastitis Clínica es del 15%, mientras que en los hatos con altos niveles de CCS la mastitis clínica esta presente en un 33%. ¿Si seleccionamos al azar en estos hatos cual es la probabilidad de escoger un animal positivo para mastitis clínica?

• Probabilidad vaca con MC = P (mastitis|bajo SCS) * P(bajo SCS) + P(mastisis|alto SCS) * P(alto SCS)


• Probabilidad vaca con MC= (0.15*0.60)+(0.33*0.40)


• Probabilidad vaca con MC= 0.09+0.132= 0.22

3.10- Regla de la adición de las probabilidades

Esta regla calcula la probabilidad de la unión de un evento A y un evento B y está basada en la probabilidad de los conjuntos individuales, calculando el tamaño de la unión y descontando el tamaño de la intersección.

P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

Ejemplo, en un análisis de casos en una clínica veterinaria se encontró que el 15% de los pacientes caninos que atendieron consulta el año anterior eran hipertensos. El 6% de los pacientes fueron pacientes con fallo renal y el 3% de los casos atendidos presentaron ambas situacion (hipertensión y falla renal). ¿Que probabilidad existe de que se seleccione un paciente que sea hipertenso o con fallo renal?

• P(Hipertenso ∪ Fallo Renal) = 0.15 + 0.06 – 0.03
• P(Hipertenso ∪ Fallo Renal) = 0.18%

3.11- Regla de la multiplicación de las probabilidades

Esta regla nos permite encontrar la probabilidad de que ocurra el evento A y el evento B. Para la regla de la multiplicación existen dos casos, el primero se da si los eventos son dependientes y el segundo cuando los eventos son independientes. Veamos entonces como se diferencian:

3.11.1- Eventos dependientes

La regla de la multiplicación para eventos dependientes se da cuando los eventos están relacionados entre sí. La fórmula esta definida de la siguiente manera:

P(A ∩ B) = P(B) * P(A|B)

Donde la probabilidad esta dada por la probabilidad de A dado que B ocurrió y multiplicado por la probabilidad de B.
Por ejemplo, si voy a sacar dos novillas de un corral donde hay 4 blancas, 5 pardas y 2 negras, cual es la probabilidad de que la segunda novilla sea negra sabiendo que la primera también fue negra (no hay reemplazos dentro del corral).
El espacio muestral en este caso sería de: 4 novillas blancas + 5 novillas pardas +2 novillas negras = 11 novillas, entonces

En la primera sacada hay dos novillas negras de un total de 11 novillas. En la segunda hay una de un total de 10 novillas, entonces, la posibilidad de que salgan los dos animales negros en primer y segundo lugar es apenas del 1.8%.

3.11.2- Eventos independientes

En el segundo caso de la regla de la multiplicación, los eventos son independientes cuando la ocurrencia de uno de ellos no afecta la ocurrencia del otro. la fórmula se expresa de la siguiente manera:

P(A ∪ B) = P(A) * P(B)

Por ejemplo, en una finca hay 100 novillas de las cuales 35 son Holstein. De las 100 novillas 75 han sido inseminadas por primera vez. El hecho de que la novilla sea Holstein no tiene nada que ver con que la novilla haya sido inseminada o no. Ahora nos interesa saber,cuál es la probabilidad que una de las novillas Holstein haya sido inseminada?

Entonces, La probabilidad de seleccionar una novilla Holstein que haya sido inseminada dentro de la totalidad de las 100 novillas es del 26%.

3.12- El teorema de Bayes

El teorema de Bayes es utilizado para calcular la probabilidad de un suceso, teniendo información que de antemano se conoce sobre ese suceso (Lopez,2018). Entre las muchas aplicaciones del teorema de Bayes es de mucha utilidad para ayudarnos a encontrar una relación causal entre dos eventos, es decir nos ayuda a buscar argumentos mas razonables acerca de que evento puede causar el otro. Por ejemplo nos ayuda a establecer una enfermedad a partir de una serie de síntomas. También es muy útil a la hora de determinar la probabilidad de que un paciente padezca realmente una enfermedad cuando tenga un test positivo.

Por ejemplo, en una región lechera en Colombia la prevalencia histórica de la leucosis bovina es del 10%. En esta misma región se va a ensayar una nueva prueba diagnóstica PCR y se sabe que su sensibilidad (animales enfermos con un test positivo) es del 95%, mientras que su especificidad (animales negativos con un test negativo) es del 50%. Para esta región si un animal da positivo en la prueba, cuál es la probabilidad de que el animal sea realmente positivo a leucosis viral bovina?

Entonces tenemos que:

• P(A) = 0.1 (prevalencia de animales enfermos en la región)
• P(S) = 0.9 (animales sanos o libres de leucosis viral bovina)
• P(B|A) = 0.95 (animales positivos al test que padecen la enfermedad -sensibilidad-)
• (B|S) = 0.05 (animales positivos al test que estan sanos)
• (B) = P(B|A) * P(A) + P(B|S) * P(S)
• (B) = 0.95 * 0.1 + 0.05 * 0.9 = 0.1405
• P(A|B) = ?

P(A|B) = (0.95 * 0.10) / 0.1405 = 67.61%

Entonces la probabilidad de que un animal positivo a la prueba PCR sea portador del virus de la leucosis bovina es del 67.61%. Esto nos da una idea de la importancia de poner los resultados en contexto, ya que el 95% de sensibilidad de la prueba, no da un margen de error y hay que tenerlo en cuenta, así como la prevalencia o la incidencia de la enfermedad en la región.