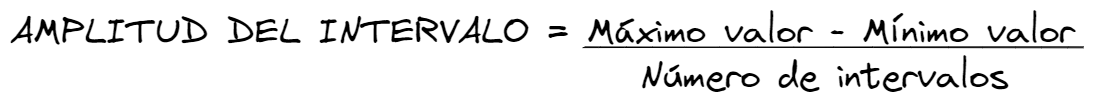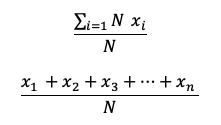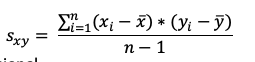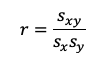Vet Análisis Datos
Tal como se ha hablado anteriormente los datos que se recogen en la finca o en cualquier otro tipo de actividad que los genere, tienen diferentenaturaleza. En esta sección vamos a revisar como visualizar estos datos para poder entenderlos mejor y saber que nos dicen y también veremos como podemos realizar una aproximación a la estadística descriptiva utilizando herramientas sencillas en la hoja de cálculo Excel.
Los datos categóricos son datos que se dividen en grupos, como por ejemplo, sexo (masculino, femenino) o raza (holstein, pardo suizo, normando). Veamos como podemos mostrar y resumir los datos categóricos con un ejemplo práctico. Por ejemplo, de una clínica veterinaria obtenemos una lista de historias clínicas de perros (n= 89). Queremos clasificar los animales por su tamaño, entonces, para ello los hemos dividimos en tres categorias: grande, mediano y pequeño. De esta manera ya podremos cuantificar el número de animales que pertenecen a cada categoría y comenzar a entender por ejemplo, que pacientes son los que mas atiende la clínica de acuerdo con su tamaño.
Para cuantificar en Excel podemos utilizar varias alternativas, una de ellas son las tablas pivotantes (pivot tables). Estas tablas son una herramienta muy práctica y flexible para resumir información y nos dan la opción de cuantificar y visualizar las variables incluidas. Otro recurso útil es trabajar con las funciones creadas por Excel. En este caso la primera que podemos explorar para contar el número de animales para cada una de las categorias de la variable 'Tamaño' es la función =CONTAR.SI o =COUNTIF en inglés. Como siempre que vamos a usar una función primero nos ubicamos en la celda donde queremos la información, luego digitamos la función (=CONTAR.SI), y seleccionamos el rango donde están nuestros datos, separamos con una coma (,) y posteriormete seleccionamos el criterio por el cual deseamos clasficar. Es decir escribimos la condición, que para este caso sería celdas que en el rango que estamos buscando contengan la G o sea animales de tamaño grande tal como se muestra el cuadro inferior.
Completamos la información para cada una de las categorias y de esta manera obtenemos la tabla que resume el número de animales por categoría.
Es una de las gráficas mas comunes para la visualización de datos categóricos ya que permite visualizar la información de manera sencilla. Como se observa en el diagrama inferior este gráfico es una representación de la tabla presentada en el cuadro superior. Cada barra representa una categoría y en el eje vertical se presenta la distribución absoluta (conteo). Para hacerlo en Excel simplemente seleccionamos los datos, y desde el menú 'Insertar' que se encuentra en la parte superior y se escoge las gráfica deseada (en la barra superior se selecciona por los íconos que las represatan). En este caso seleccionamos la opción (columnas), el menú de opciones es amplio por lo que hay mucha flexibilidad en el diseño.
Se utiliza para mostrar que porcentaje del total (100%) ocupan las diferentes categorias. De la totalidad de animales de la muestra en que porcentaje están representados los grandes (G), los medianos (M) y los pequeños (M). En Excel la forma de obtener este gráfico es similar al anterior. Seleccione los datos, de ahi ir a 'Insertar', y finalmente seleccionar el ícono de la torta que mas se ajuste a sus necesidades pues hay en 2D o en 3D y la puede ajustar a su gusto.
Los datos nominales también se pueden presentar con un diagrama de Pareto. Este presenta las barras verticales que muestran la frecuencia absoluta de unidades por valor que toma la variable (cantidad de perros G, M o S) y simultáneamente en un eje vertical secundario (a la derecha va indicando la frecuencia acumulada relativa (porcentaje) con que cada valor contribuye hasta lograr el 100% (línea naranja). De igual manera es posible realizar el diagrama de Pareto en Excel seleccionando la opción en el menú de gráficos.
Los datos cuantitavos son aquellos que podemos expresar de forma numerica. Con estos datos hay mas posibilidades y flexibilidad en la manera como podemos presentarlos y la vez entenderlos. Una manera frecuente de presentar los datos cuantitativos es la utilización de tablas de distribución de frecuencias o histogramas. A diferencia de los nominales donde para crear el diagrama de barras básicamente cada valor que toma la variable (Caso anterior G, M, S) representa una columna, cuando trabajamos con información cuantitativa creamos intervalos del mismo tamaño que nos sirven para agrupar el conjunto de los datos basados en los valores que toma la variable. Esto nos permite presentar de manera resumida la información. En la tabla se aconseja no solo presentar la frecuencia total sino también la frecuencia relativa (porcentajes). Por ejemplo, vamos a presentar una tabla que resuma la producción de leche ajustada a 305 días por lactancia de una finca lechera. Lo primero que debemos hacer es conocer el valor mínimo y el valor máximo (12150 y 47820 respectivamente), luego decidir el número de intervalos y ahi podremos calcular la amplitud del intervalo con la siguiente fórmula:
Si estamos trabajando con una tabla con muchos datos, encontrar los valores máximo y mínimo puede ser asunto complicado. Podemos encontrar estos valore con funciones de Excel para ello utilizamos las funciones =MIN() y =MAX() respectivamente. Dentro de la función seleccionamos la ubicación del rango de valores que toma la variable en la tabla. Una vez encontrados estos valores reemplazando la fórmula tenemos:
Esto quiere decir que vamos a construir una tabla con 10 intervalos con una amplitud de 3567 libras cada uno, comenzando con el inferior que será desde el valor mínimo 12150 libras + 3567 libras, así que el primer el primer intervalo será desde 12150 hasta 15717 y así sucesivamente hasta el último rango que será desde 44253 hasta 47820 (valor máximo). Excel tiene una herramienta muy práctica para la construcción del histograma de frecuencias. Para ello asegúrese de tener instalado la herramienta de 'Análisis de Datos' o 'Data Analysis' en el menú 'Datos' o 'Data' que se halla ubicado en la parte superior de la pantalla.
Una vez que hemos definido los intervalos y sabemos la amplitud de estos hacemos una columna con ellos como se muestra en la tabla que se muestra a conticuación, teniendo presente que incluimos los valores máximos de cada intervalo. Es decir, para el primero que sería de 12150 a 15717, solo digitamos el 15717, sigue 19284 y así hasta el último. Posteriomente vamos al menu datos, seleccionamos data analysis y finalmente histogram.
Inmediatamente se abre una hoja de diálogo y lo primero que se pide es seleccionar el rango de celdas donde están nuestros datos (Input Range). Posteriormente seleccionamos los intervalos que acabamos de construir (Bin Range). También tenemos la opción de seleccionar si queremos los datos en una nueva hoja o podemos asignar una hoja específica y finalmente podemos escoger si queremos un diagrama de Pareto, una secuencia acumulativa o simplemente el gráfico con el histograma. Damos ok y podemos ver el reporte de frecuencias y la gráfica como se muestra en el diagrama y la tabla. Existen otras alternativas en Excel de crear histogramas por ejemplo utilizando la opción CONTAR.SI y FRECUENCIA de manera que esta no es la única pero tal vez la mas rápida.
Como se observa el reporte obtenido nos devuelve los invervalos con la cantidad de lactancias en cada intervalo y el porcentaje que representa cada una del total. De igual manera nos entrega el siguiente histograma de frecuencias:
Para entender como se relacionan dos variables cuantitativas, un primer paso es la visualización y para ello podemos utilizar los gráficos de dispersión, posteriormente veremos la manera de medir que tan estrechas son estasrelaciones. Este tipo de gráfico es muy útil para entender si dos variables tienen algún tipo de relación. Como ejemplo, el siguiente gráfico presenta la cantidad de grasa producida (eje horizontal) y la producción de leche (eje vertical) para un grupo de vacas de 1ª lactación.
Como se observa en el gráfico parece que existe una tendencia lineal entre la producción de grasa en leche y el volumen total de leche (a mayor leche mayor cantidad de grasa), sin embargo este es solo un primer ejercicio para tratar de entender los datos de que disponemos. Luego tendremos que confirmar con fórmulas de asociación como correlaciones o covarianzas. Para realizar el gráfico en Excel, necesitamos seleccionar los rangos donde se encuentran los datos y luego del menú insertar gráficos seleccionar "scatter" o dispersión.
Las tablas cruzadas o tablas de contingencia son ideales para resumir y visualizar los datos de las variables categóricas. En la tabla cruzada un grupo de categorías va en el eje horizontal (X) y otro grupo en el eje vertical (Y). Por ejemplo, si utilizamos una base de datos de un albergue de datos (datos obtenidos deKaggle) y seleccionamos las dos variables categóricas disponibles que son animales esterilizados cuyas categorias (si, no) ubicamos en el eje horizontal y para la variable sexo, ubicamos sus categorias (Macho, Hembra) en el eje vertical. También es importante incluir los totales. Para este tipo de tabla es muy útil utilizar las tablas dinámicas de Excel que nos permiten no solo realizar la tabla, sino también visualizar el gráfico.
Siguiendo la metodología descrita en el enlace de como crear una tabla dinámica cruzamos los datos de sexo y esterilización. En este caso decidimos mostrar la información por totales sin embargo podemos mostrar tambien sus valores relativos. De igual manera podemos seleccionar la opción de visualizar los datos en una gráfica dinámica.
Cuando se obtiene una colección de datos de cualquier naturaleza, al inicio, el estado original de los datos pueden no mostrar mucho sobre lo que nos interesa buscar o lo que podemos encontrar. Es por ello que es necesario organizar y simplificar los datos de una manera en que ya sea a manera de tablas, gráficos u otros medio (promedios, porcentajes, totales), podamos comenzar a realizar una adecuado análisis e interpretación de la información (Pfaffenberger, R.C. and Patterson, J.H., 1977).
Entonces, podemos decir que la estadística descriptiva se encarga del resumen y descripción de los datos. El análisis descriptivo se limita únicamente a los datos coleccionados (muestra) y no realiza inferencia o generalización acerca de la totalidad de donde provienen las observaciones seleccionadas (población) (Chao, 1977). Como hemos venido insistiendo, antes de embarcarnos en cualquier análisis, debemos primero comprender la naturaleza de los datos y de acuerdo con ello que tipo de medición hacemos como vimos anteriormente en la 'clasificación de los datos según su naturaleza'. Revisemos a continuación algunos conceptos básicos de estadística descriptiva que nos serviran para entender de manera mas clara los datos la naturaleza de los datos con los cuales estaremos trabajando
La Media es la mas común de todas las medidas de tendencia central. Simplemente es el promedio de los datos. La media representa el centro físico del conjunto de datos y se define como la suma de los valores observados, dividido por el total de observaciones (Chao,1978). En Excel =AVERAGE( ) o PROMEDIO( )
La Mediana es el valor que divide un conjunto de observaciones ordenadas respecto de la magnitud de los valores, de tal manera que el numero de datos por encima de la mediana sea igual al numero de datos por debajo de la misma (Chao, 1978). Si esta posición no es un número entero entonces la mediana es el promedio simple de los dos números mas cercanos a la posición calculada. Excel =MEDIAN()
Moda es el dato que mas se repite o se da con mayor frecuencia dentro de una sucesión de datos. La moda se halla buscando el dato que tenga la frecuencia mas alta. Excel =MODE.SNGL( ) entrega una sola moda, =MODE.MULT( ) entrega una colección de modas.
Sesgo es una medida de asimetría que indica si las observaciones del conjunto de datos se concentran en un lado de la distribución de los datos. Sesgo derecho indica que los datos se concentran hacia la derecha de la curva (la cola larga se ve hacia la derecha). Izquierda, indica que los datos se concentran hacia la izquierda de la curva. Cuando los resultados del sesgo son negativos, los resultados están desviados hacia la derecha. Al contrario, con son positivos los resultados están desviados hacia la izquierda. Excel =SKEW()
Para el análisis de datos no basta con encontrar las medidas de posición central, ya que varias muestras pueden presentar las mismas medias, sin embargo, la dispersión de los datos puede darnos claros ejemplos de el comportamiento de los mismos. Las medidas de variabilidad nos indican el grado de dispersión en un conjunto de datos. Si este valor es pequeño entonces hay uniformidad en los datos. Por el contrario habrá poca uniformidad. Si es cero, entonces todos los datos son iguales. Por ejemplo, no es igual tener un lote de pollos de engorde con una media de 2.2 kg y una desviación estándar de 0.3 kg, que un lote de pollos de engorde con una media de 2.2 kg y una desviación estándar de 0.6kg. A pesar de que las medias son iguales los datos del segundo lote estan mucho mas dispersos, por tanto la uniformidad estaría mas comprometida lo cual puede representar pérdidas económicas. Las medidas de dispersión de mas frecuente uso son:
La razón fundamental por la que no se toma el promedio de las desviaciones como medida de variabilidad es que la suma de las desviaciones siempre arroja 0. Esto se soluciona con la varianza elevando al cuadrado las diferencias entre los datos y la media y dividiendo por la cantidad de datos (N)si es varianza poblacional o (n-1) si es varianza muestral. En Excel usamos =VAR.S() para varianza muestral y =VAR.P() para la varianza poblacional.
Varianza poblacional Excel =STDEV.P()
Varianza muestral Excel = STDEV.S()
Varianza poblacional Excel =STDEV.P()
Varianza muestral Excel = STDEV.S()
1 of 2
La varianza es el promedio de los cuadrados de las desviaciones. Al tomar el cuadrado de las desviaciones para el calculo de la varianza, las unidades en estén dados los datos también se expresarán en unidades al cuadrado. Esto puede no tener sentido, es por ello por lo que se modificó para obtener las unidades reales y se llegó al concepto de laDesviación Estándar. La desviación estándar, es la raíz cuadrada de la varianza y es la medida de variabilidad de mayor uso para calcular la dispersión de los datos. En Excel la función es '=DESVESTA' o '=STDEV' en inglés.
Para continuar con la introducción al análisis de los datos vamos a trabajar con el paquete de herramientas de análisis de datos de Excel. Este paquete se instala de manera muy sencilla y nos permite realizar varios tipos de análisis desde estadística descriptiva hasta analisis de varianza y regresiones múltiples. Para entender su instalación y su funcionamiento por favor revise el video que se encuentra a continuación.
En una producción porcícola se obtienen los resultados de peso y consumo de alimento de los últimos 100 cerdos vendidos. Los datos se encuentran en una tabla de Excel y queremos ver que podemos obtener de ellos. La tabla que se presenta a continuación muestra un fragmento de los 10 primeros animales.
Recordemos que la conversión es un dato calculado que mide la cantidad de alimento utilizado por unidad de peso (en este caso kg) ganado. La fórmula general de la conversión es:
Lo primero que vamos a hacer es el cálculo de las medias. Podemos utilizar la función =PROMEDIO o =AVERAGE y seleccionar el grupo de datos como se muestra en la tabla. La misma operación para para la mediana=MEDIAN o =MEDIANA y la moda =MODE o =MODA. Es importante anotar que MODE es considerado por Excel como una variable en modo compatibilidad. Por ello se recomienda utilizar =MODE.SNGL para el número que ocurre con mayor frecuencia o =MODE.MULT que muestra la serie de números que ocurren con mayor frecuencia. Ojo si no hay duplicados dentro de la serie de datos el resultado será N/A.
Los valores máximos y mínimos los calculamos con las funciones =MAX() y =MIN(). Para el sesgo utilizamos la función =SKEW o en español =COEFICIENTE.ASIMETRIA.P. La función de la varianza es =VAR.P o =VAR.S ya sea para una población o para una muestra respectivamente. Para Excel en español =VARS para una muestra y =VARP para la población. La desviación estándar de igual manera =STDEV.P o STDEV.S para población o muestra respectivamente, si Excel ha sido configrado en inglés (como en mi caso) o si es en español entonces las funciones son =DESVESTP para población y =DESVESTpara la muestra en caso de dudas sobre como escriben las funciones se puede consultar este enlace. Con todas estas variables podemos crear nuestro reporte en una tabla:
Excel tiene incorporada una herramienta para hacer análisis descriptivo de manera rápida, para ello debemos instalar la herramienta de análisis de datos. Una vez instalada seleccionamos la opción estadística descriptiva o “descriptive statistics”, inmediatamente se abre una hoja de dialogo donde debemos seleccionar el rango de datos que deseamos incluir y aclarar si los datos están por columnas como en este caso y si las columnas tienen etiquetas (labels). Seleccionamos además la ubicación del informe y finalmente que tipo de análisis estadístico deseamos ver, en este caso nos quedamos con el resumen estadístico (summary statistics).
Finalmente La tabla siguiente muestra los resultados del informe generado por Excel.
Como se observa es un informe bastante completo que se puede generar rápidamente y permite hacer una aproximación rápida a los datos que estamos comenzando a analizar. El informe presenta en una tabla las medidas de tendencia central, las medidas de dispersión, los valores mínimos y máximos asi como la cantidad de datos para cada una de las variables seleccionadas.
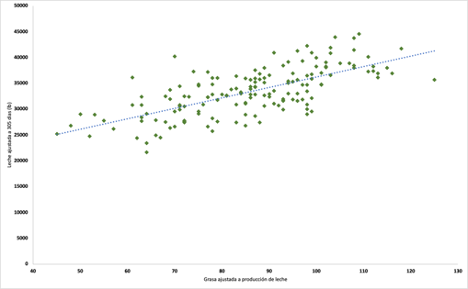
En la sección 5.3 vimos algunas maneras como podemos visualizar si existe alguna relación entre dos variables. Ahora veamos como se puede medir el grado de relación entre dos variables
La covarianza es una medida de variabilidad conjunta de dos variables. Si la covarianza es positiva esto indica que las dos variables se mueven juntas en la misma dirección. Si la covarianza es negativa entonces las dos variables se mueven en direcciones opuestas. Si la covarianza es 0 las dos variables son independientes la una de la otra. La covarianza puede tomar valores hasta el infinito tanto positivos como negativos. Esto es un problema porque dificulta entender que tan ligadas están las dos variables.
Para la covarianza muestral tenemos que X es la media de la variable X, x i es la "iésima" posición de esta variable, mientras que Y representa la media de la variable Y, yi representa la "iésima" posición de la variable y. Finalmente n representa el número total de observaciones (suma de observaciones de X y Y).
En Excel para la covarianza muestral se utiliza la función =COVARIANCE.S si la configuración está en inglés o =COVARIANZA.M en español. Para la covarianza poblacional las funciones son =COVARIANCE.P o =COVARIANZA.P respectivamente.
La correlación es una medida de variación conjunta de dos variables. La correlación busca estudiar el grado de asociación entre variables. También se conoce como correlación lineal de Pearson, es una medida de regresión lineal que pretende cuantificar el grado de variación conjunta entre dos variables. Es importante aclarar que dos variables que están altamente correlacionadas no necesariamente implican que una es causal de la otra (correlación no implica causalidad).
A diferencia de la covarianza, es una medida estandarizada que toma medidas entre -1 y +1 de manera que es mas fácil de interpretar los resultados. Donde valores positivos indican que, si el valor de x sube, el de y sube. Al contrario, si el valor es negativo indica que si x aumenta, y disminuye y un valor 0 es que no hay correlación.
En Excel para la correlación la función =CORREL tanto en español como en inglés
Donde Sxy representa la covarianza entre las variables X y Y (ver fórmula anterior), Sx es la desviación típica de X y Sy es la desviación típica de Y.
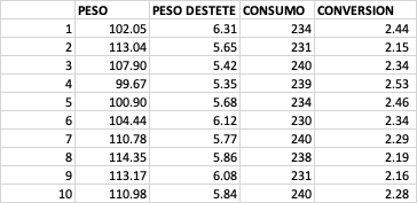
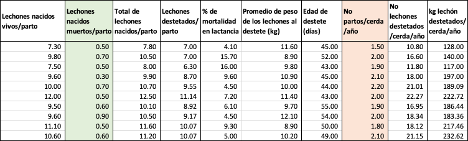
Tenemos los promedios de los registros de producción de 10 granjas de cerdas de cría de una región de Caldas (Colombia) como lo muestra el registro a continuación.
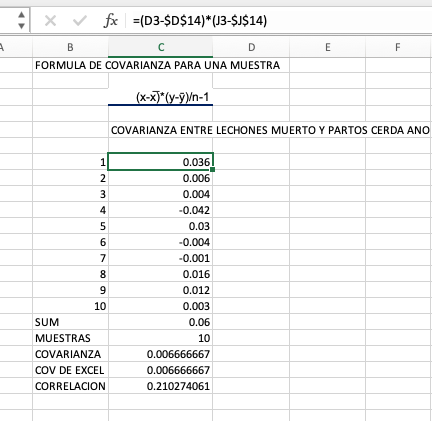
Queremos calcular la covarianza entre lechones nacidos muertos o mortinatos por parto (columna verde) y el número de partos por cerdas por año (columna naranja). Podemos seguir la fórmula de la covarianza muestral y hacer los cálculos en Excel, o bien podemos utilizar la función =COVARIANCE.S (). El resultado va a ser igual como se observa.
El resultado de la covarianza es positivo 0.0067 lo que nos indica que si hay mas animales por camada tambien hay mas mortinatos por camada. Para cuantificar que tan cercana es la relación entonces acudimos a la correlación, para ello tambien podemos correr la formula o simplemente utilizar la función = CORREL de Excel como se muestra en la tabla superior.
