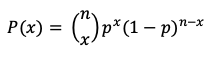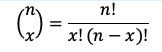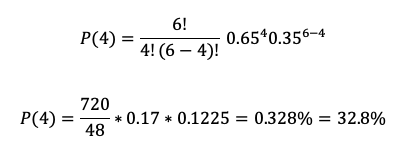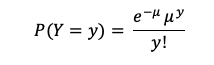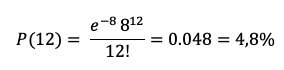4.3.4- Distribuciones discretas-Poisson
Cuando queremos saber la probabilidad de un determinado evento Y, que ocurre en un intervalo de tiempo, distancia, área o volumen definidos usamos la distribución de Poisson.
Y∼℘(μ)
La distribución de Poisson solamente depende de un parámetro μ. Tanto la media como la varianza de esta distribución son siempre positivas. Se utiliza para determinar que tan posible es un resultado específico, conociendo con que frecuencia este evento ocurre usualmente. Con la distribución de Poisson podemos hacer planificación de espacios, tiempos, áreas o cualquier otro aspecto que implique un evento que ocurra en un espacio/tiempo/área determinada. Por ejemplo:
-
- Número de pacientes que necesitan cirugía en una clínica
veterinaria por día (planeación de quirófano).
-
- Número células somáticas por mililitro en leche (identificación de
problemas de mastitis clínica).
-
- Número de partos en una piara por mes (planificación de número de
parideras en la finca).
La fórmula de la distribución de Poisson es:
donde:
- P(Y=y) es la probabilidad de y en el intervalo definido
- μ es el valor esperado o media de y
- e es la base de los logaritmos naturales (2.71828)
Ejemplo: en una producción porcina el promedio de partos a la semana es de
8 (tasa de partos del 85% y 2.4 camadas/año). Si se mantienen los mismos índices
cual es la probabilidad de tener 12 partos en una semana sabiendo que en este
momento la máxima capacidad planeada de parideras es de hasta 11 partos?
- y= 12 partos/s
- μ = 8 partos/s
A pesar de que la probabilidad no es tan alta (~5%), si proyectamos esa probabilidad a un año es posible que en aproximadamente 3 semanas al año (2.6) se nos presente este problema y si se incrementa la tasa de partos, pues seguramente el propietario se verá forzado a incrementar la capacidad instalada. Pero por ahora tal vez no haya necesidad de ampliar si existen otras prioridades.
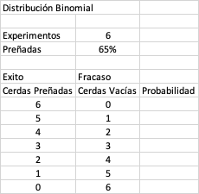
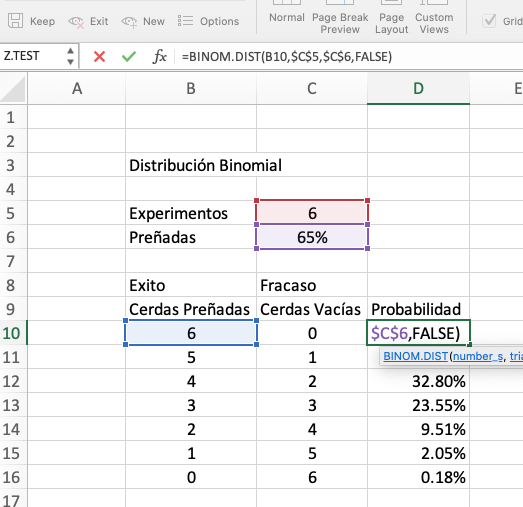
Al igual que con la distribución Binomial, Excel nos permite calcular
las probabilidades de esta distribución utilizando la función DISTR.POISSON o POISSON.DIST en inglés. Entonces si queremos construir este tipo de distribución en
Excel, lo mas práctico es hacer una tabla con los valores para los cuales
deseamos calcular la probabilidad e incluir la media. Como se muestra en
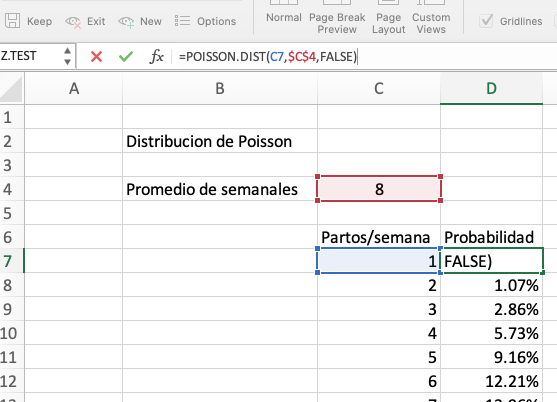
la ilustración, nos ubicamos en la celda donde deseamos ubicar la probabilidad,
se escribe la función =POISSON.DIST. Si observamos la captura de
pantalla ubicada en la parte inferior La función nos va primeo a pedir
que insertemos la probabilidad de que ocurra el evento. Esta está
ubicada en la celda C7 (probabilidad de un parto a la semana), luego la
media de partos semanales que está en la celda C4 y finalmente la opción
acumulativa (TRUE o VERDADERO) o si no queremos acumulados FALSO
(FALSE).
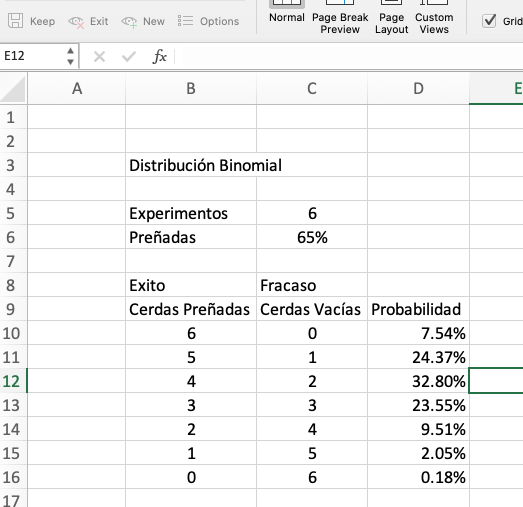
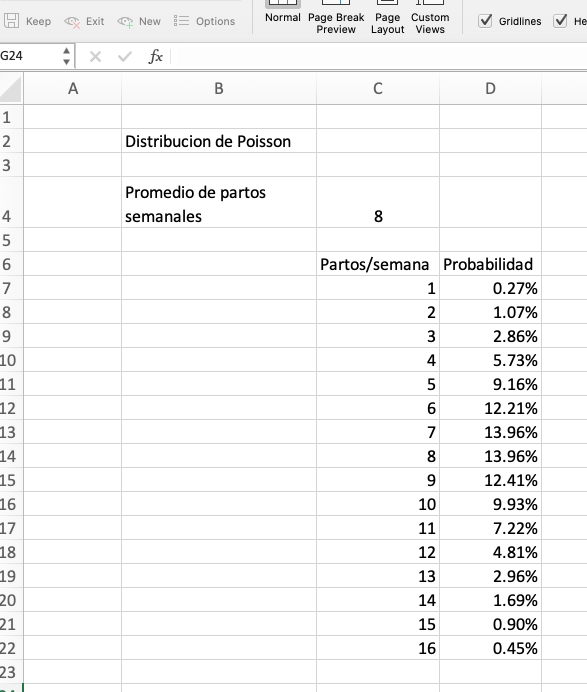
Realizamos el mismo procedimiento para los demás valores (estiramos la
función) tal como hicimos con la distribución
Binomial y de esta manera
obtenemos nuestra tabla con las probabilidades de partos a la semana:
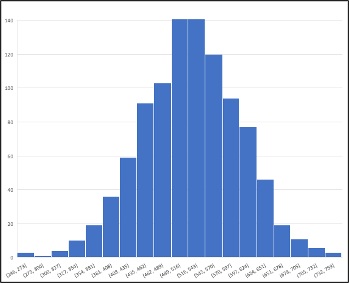
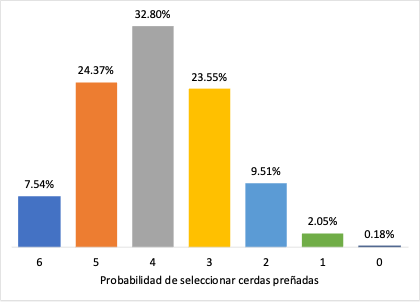
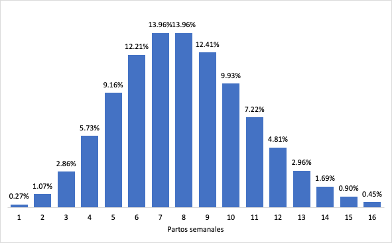
Utilizando el diagrama de barras podemos visualizar la curva de la
distribucion de Poisson para el ejemplo anteriorEjemplo de una distribución de Poisson en Excel
 Vet Análisis Datos
Vet Análisis Datos