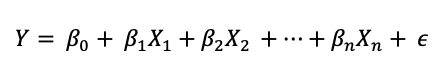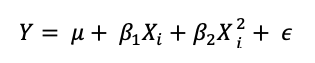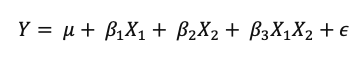7.10- Variables nominales y construcción de variables ficticias
Como hemos visto en los casos anteriores, en las regresiones lineales
utilizamos variables continuas como variables independientes. De acuerdo
con el efecto que tienen estos predictores pueden haber interacciones o
efectos cuadraticos (tambien pueden haber efectos cúbicos pero no serán
tratados aquí. Sin embargo, también es posible utilizar variables
nominales
en el análisis de regresión múltiple. Por ejemplo, variables nominales
como el número de la lactancia en ganado vacuno o el número del partos en
cerdas de cría. También dicótomas como el sexo en ganado de ceba que pueden
jugar un importante papel en consumo de alimento o la ganancia de peso, por
tanto no pueden ser excluidas. Estas variables siempre se deben tratar como
como un código binario 0 y 1 y para ello se crean las variables ficticias
(dummy variables).
Como el modelo solo acepta valores de 0 y 1, cuando tenemos variables con
mas de una categoría debemos crear variables ficticas que representen las
comparaciones entre los diferentes grupos (razas, región etc.). El grupo
de variables ficticias son consideradas en el modelo de regresión simultáneamente
como un conjunto de variables independientes. Suponga que queremos medir
en una granja de cerdos los niveles en hormonas de la reproducción en las
diferentes hembras que hay en la granja. Actualmente en la granja hay cerdas
de las razas Pietrain, Landrace, Duroc y Poland-China. Esta variable tendría
4 categórias pero se construyen solo tres variables ficticias. Para considerar
entonces raza como predictor en un modelo de regresión, se deben crear tres
variables indicadoras (una menos que el total) para representar los cuatro
diferentes grupos. Para crear el conjunto de variables, primero entonces
hay que decidir un grupo referencia o categoría, es decir en este caso una
raza que se comparara contra los otros grupos. Es por esto que se construye
una una menos ya que si todas las demas variables independientes son 0, se
entiende entonces que los individuos pertenecen a la categoria base. Las
variables ficticias son creadas para los demás grupos y se codifica con 1
para los participantes que pertenecen a ese grupo y todos los demás son código
0. En el modelo de regresión múltiple, los coeficientes de regresión asociados
con cada una de las variables “dummy” son interpretadas como la diferencia
esperada entre la media esperada de ese grupo comparada con el grupo de referencia,
cuando todos los otros predictores se mantienen constantes.
Para variables dicótomas como sexo bastaría crear una sola variable por ejemplo
la variable “Hembra” entonces asignamos el valor 1 en caso de que sea hembra
y 0 para macho. No es necesario crear la variable “Macho” pues ya sabemos
que si es 0 en la variable “Hembra” es macho y entonces en el modelo estaríamos
utilizando como grupo referencia la variable macho y comparando en cuanto
difiere la hembra.
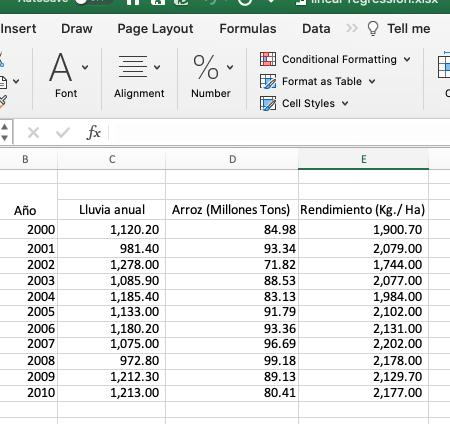
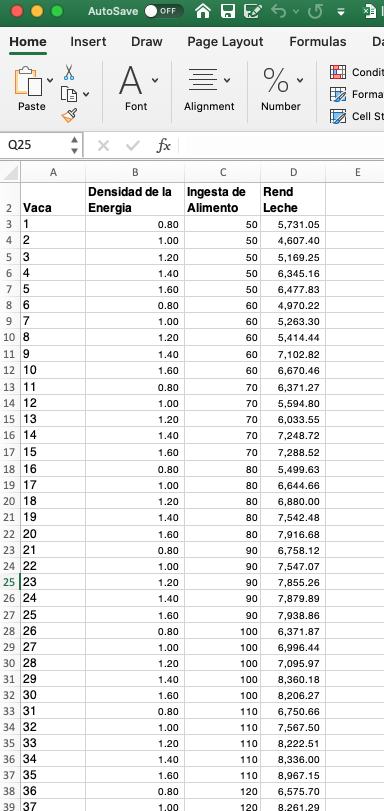
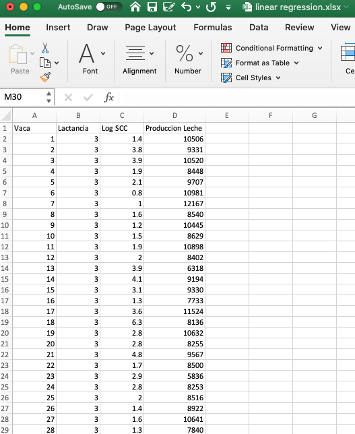
Ejemplo en Excel: Tenemos 1657 registros de vacas lecheras de un solo hato,
y deseamos establecer cual es la diferencia entre lactancias de la 1ª a la
3ª, también tenemos el promedio logarítmico del recuento de células somáticas
para cada lactación. Entonces queremos establecer un modelo donde se incluya
la lactancia como variable ficticia donde el grupo base seria la 1ª lactación
y crearíamos las variables dummy para la 2ª y 3ª lactancias. También incluiremos
el efecto de las células somáticas para ver si tienen alguno valor predictivo
sobre la producción de leche.
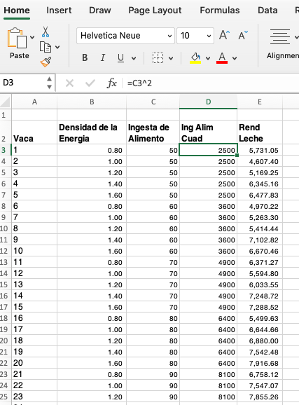
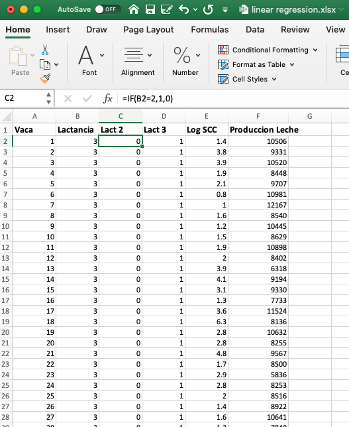
Fragmento de la tabla de datos de producción lechera, lactancias y
promedio logarítmico de recuento de células somáticas.
El primer paso es insertar dos columnas para incluir las variables ficticias.
Para crearlas en Excel básicamente podemos utilizar la función =IF, para
la lactancia 2 entonces nos ubicamos en la celda insertada para este propósito
y escribimos la función tal como se presenta en la siguiente tabla, donde
si (if) B2 (coordenada de la celda donde el registro de la variable lactancia)
= 2, entonces asigne valor 1, de lo contrario asigne valor 0. Copiamos la
fórmula en la columna y repetimos para lactancia 3.
construcción de las variables ficticias para la 2a y 3a lactación.
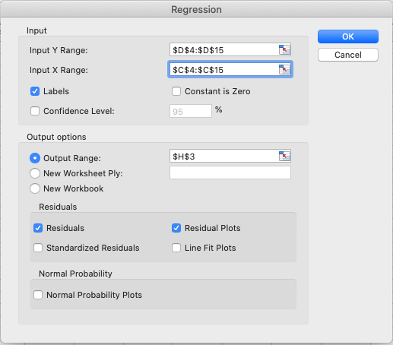
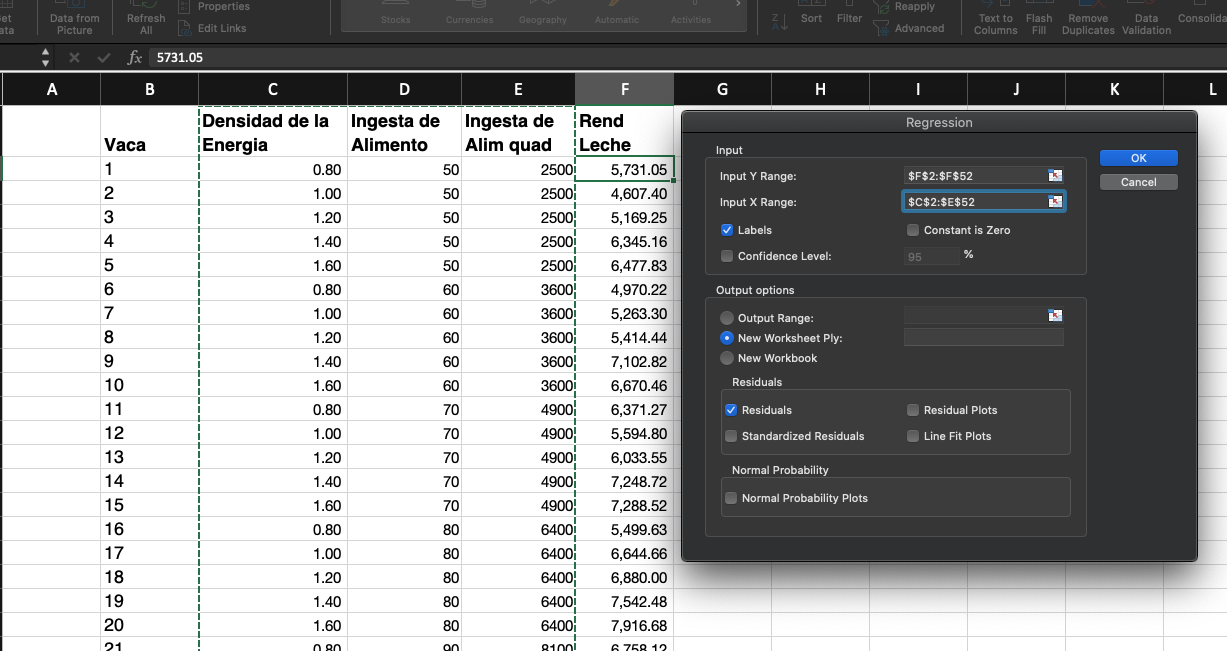
Una vez que tenemos las variables construidas, seleccionamos la herramienta
“Data Analysis” del menú datos de Excel y de ahí seleccionamos Regresión.
Seleccionamos el rango de la variable dependiente Y que en este caso es la
producción de leche y seleccionamos las variables independientes X que son
las variables ficticias que acabamos de constuir y el conteo de células somáticas,
sin olvidar que los datos tienen etiquetas y finalmente asignamos donde queremos
que se genere el reporte.
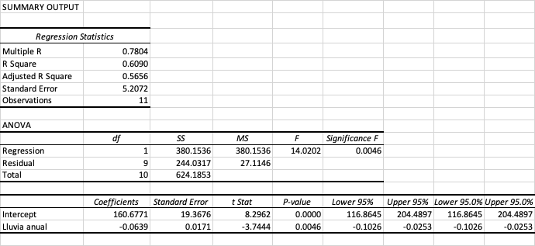
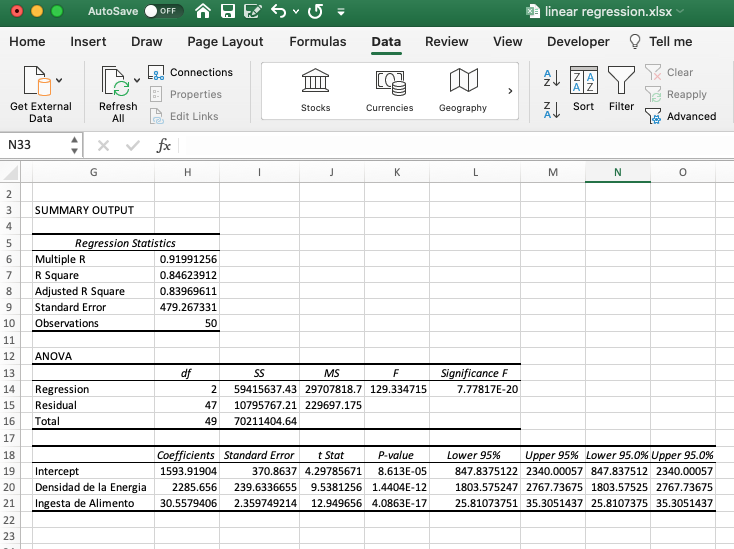
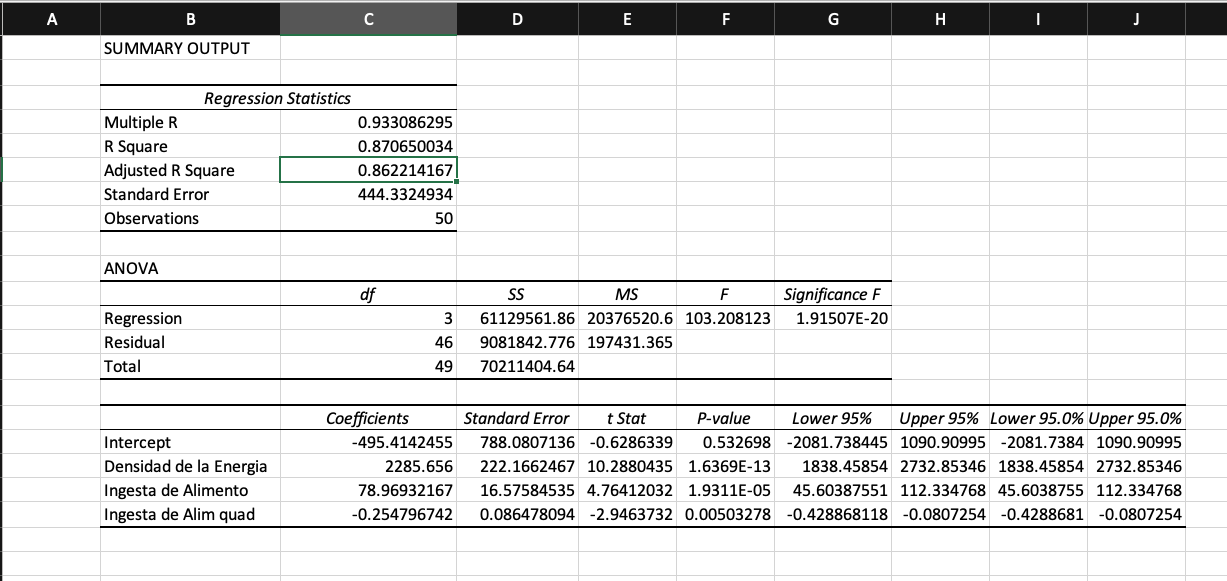
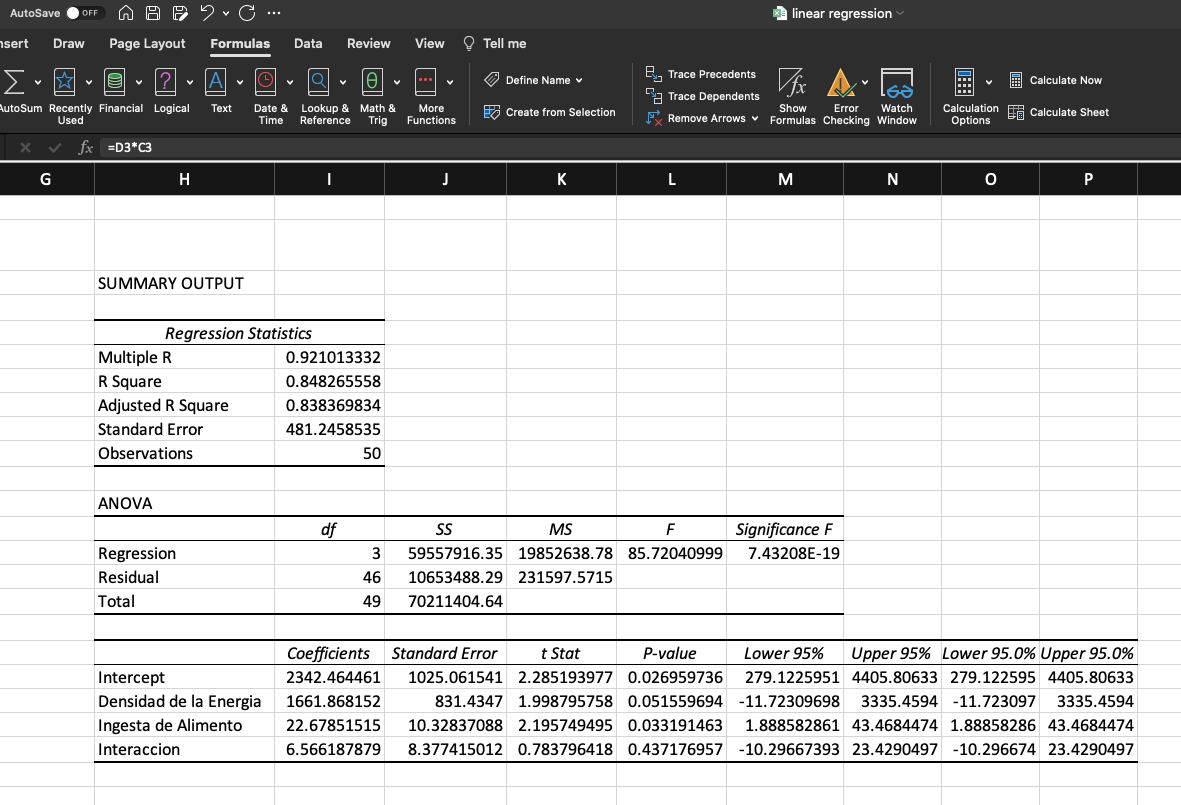
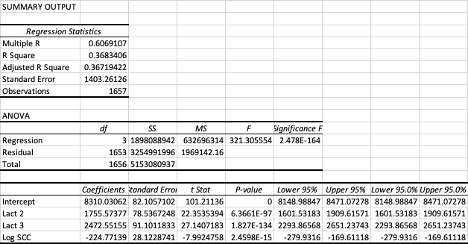
Reporte generado por Excel
El reporte generado por Excel nos presenta las tres tablas que ya conocemos.
En la tabla superior podemos ver el valor de R
2 que en este caso
es de 0.368 es decir, las variables independientes describen en un 37% el
resultado de la variable independiente. No es muy alto pero solo queríamos
conocer el peso de las lactancias así como el impacto de las de células somáticas.
La tabla 2 nos muestra el ANAVA aquí podemos ver que el modelo es significativo,
si vemos la última columna de la derecha, el valor de F es de 2.47 exponente
-164, por tanto es muy pero muy inferior al 0.05% establecido como significancia
(recordemos que si la confianza seleccionada es del 95% entonces la significancia
será del 5% o 0.05). Finalmente, en la tercera tabla podemos observar los
coeficientes. Entonces para el intercepto que seria un animal de 1
a lactancia la producción de leche estaría en 8310 kg con un error estándar
de 82. Si el animal es de lactancia 2 entonces se adicionaría 1755 kg de
leche con un error estándar de 78 kg y si el animal es de lactancia 3 entonces
al intercepto se le adicionan 2472 kg con un error estándar de 91. Las dos
variables dummy (lact 2 y lact 3) son significativas con valores P muy inferiores
a 0.05. En cuanto al valor logarítmico del recuento de células somáticas
vemos que también tiene un efecto significativo, pero este es negativo sobre
la producción de leche. Como vemos cada punto en que aumentan las células
somáticas, disminuye en 224 kg la producción de leche.
Construcción de variables tipo dummy en Excel
 Vet Análisis Datos
Vet Análisis Datos