7.4- El ANAVA factorial o de dos factores con replicación
Este tipo de ANAVA es frecuente utilizarla en diseño experimental
(bloques aleatorios) y también cuando se trabaja con mediciones
repetidas, es decir, cuando una observación ha sido hecha en el mismo
individuo mas de una vez (antes y después), por ejemplo, cuando estamos
midiendo parámetros fisiológicos o de producción en un individuo antes y
después de algún tratamiento o al aplicar un estresor como cambios de
temperatura o humedad en los galpones.
Al igual que el ANAVA sin
replicación, el ANAVA factorial con replicación se utiliza cuando
tenemos una variable medible (cuantitativa) y dos variables nominales
(factores o efectos principales) que se hallan en todas las posibles
combinaciones. En este caso tenemos tres H0 a considerar (Macdonald,2009):
-
1- Las medias de las variables medidas son iguales para los diferentes
valores de la primera variable nominal;
-
2- Las medias son iguales para los diferentes valores de la segunda
variable;
-
3- No existe interacción (los efectos de una variable nominal no
dependen de los valores de la otra variable nominal).
Se recomienda que los tamaños de las muestras de los subgrupos sean
iguales ya que esto facilita el análisis. Si queremos realizar este tipo
de prueba en Excel la herramienta Análisis de Datos (Data Analysis) lo
permite siempre y cuando el diseño esté balanceado (no pueden faltar
datos).
Por ejemplo, en una región de producción lechera en Colombia se ha establecido
un plan de mejoramiento de calidad e higiene de hatos lecheros durante cuatro
años y nos interesa ver si los planes de control e higiene en establo han
generado algún progreso entre los años 2013 al 2016. Para ello en cuatro
subregiones lecheras (variable independiente 1) contamos con los promedio
logarítmico de células somáticas (SCC/ml) de 6 hatos de representativos de
cada de cada subregion (variable cuantitativa dependiente) en donde se realizaron
las actividades de educación y control durante los cuatro años en mención
(variable dependiente 2). Entonces, una vez construida nuestra tabla, procedemos
al análisis con la ANAVA doble factorial con replicación. Para
ello tenemos todos los resultados de los 6 hatos por cada región o sea
24 datos por año durante 4 años, para un total de 96 registros (ojo no
puede faltr ningungo).
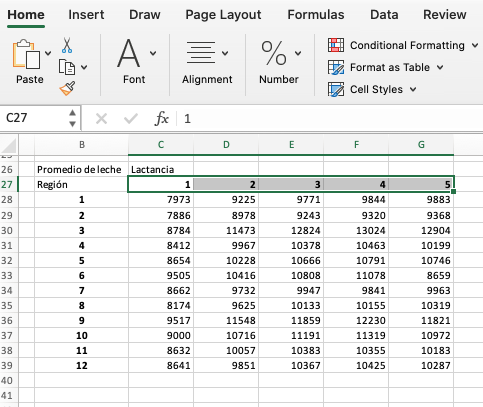
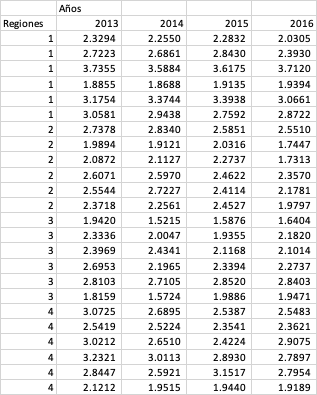
Tabla con los recuentos logarítmicos de células somáticas para 4
subregiones lecheras durante 4 años.
La tabla superior presenta el promedio logarítmico de SCC para cada uno
de los hatos distribuidos por región para cada año en cuestión. La tabla
debe estar ordenada y adecuadamente balanceada (las mismas observaciones
por variable) en este caso 6 por cada subregión, durante 4 años para
cada una de las 4 subregiones para un total de 96 registros. Una vez
tenemos nuestros datos limpios y organizados, del menú Data Analysis
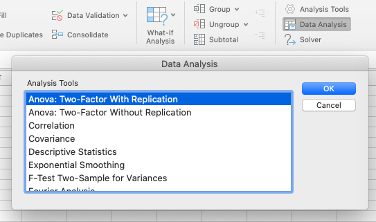
seleccionamos la opción ANOVA dos factores con replicación (ANOVA:
two-factor with replication).
En el menú de diálogo seleccionar la opción "ANOVA: two-factor with
replication" ANAVA dos factores con replicación
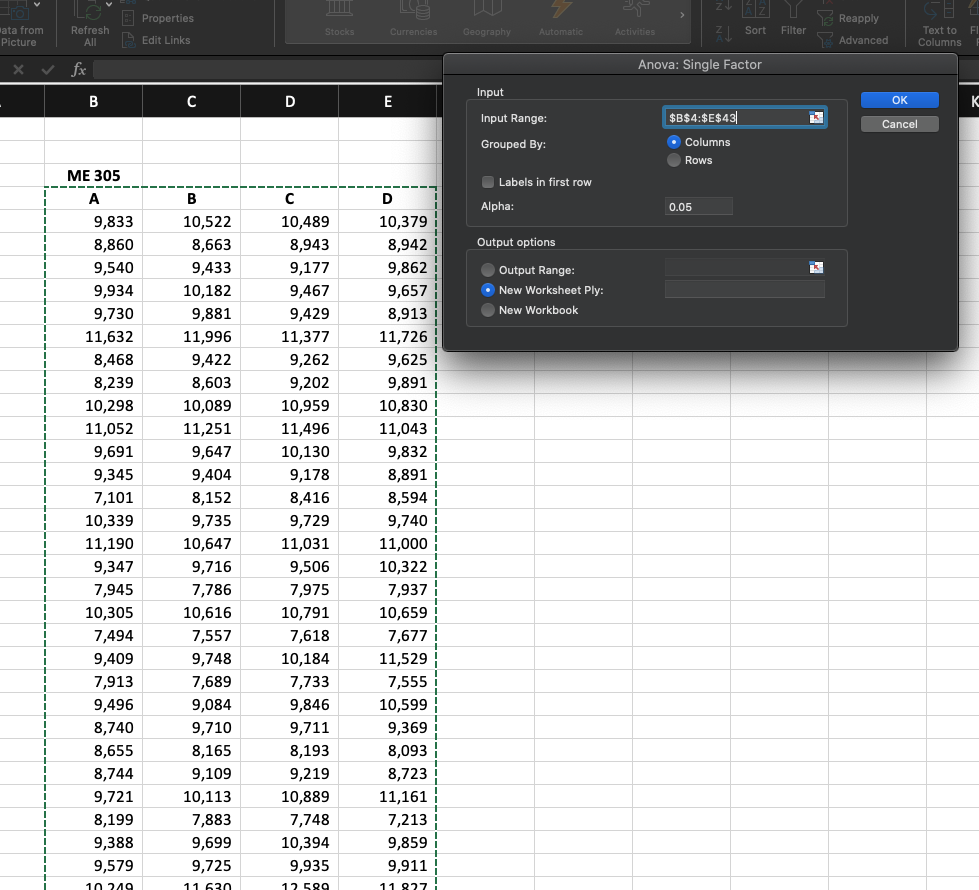
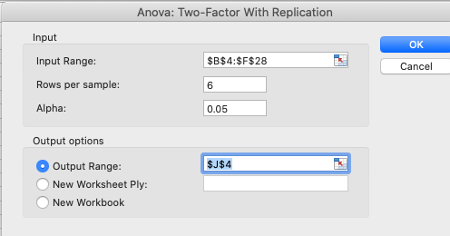
Inmediatamente se abre una hoja de diálogo que nos pide seleccionar el
rango de las celdas donde se encuentra la tabla (incluir los
encabezados), y posteriormente se debe escribir el número de filas por
cada muestra, para este caso son 6 por subregión (las subregiones están
en las filas) se debe tener en cuenta que son las mismas observaciones
para cada muestra (subregión). Luego seleccionamos el 𝛼 (0.05) y
finalmente el lugar donde se desea generar el reporte, como siempre las
opciones pueden ser dentro del página actual, en una nueva página o un
archivo diferente.
Selección de opciones para generar el ANAVA
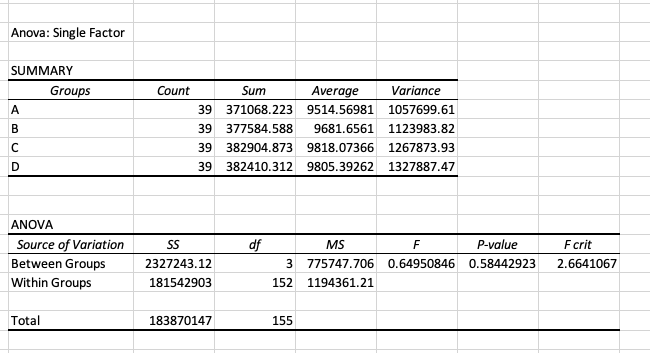
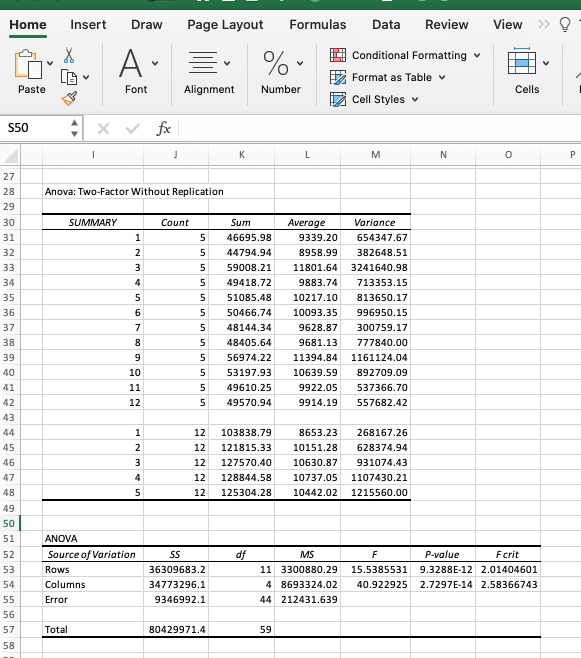
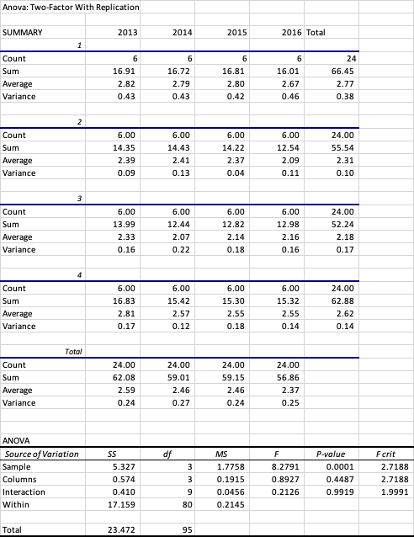
Una vez presionamos OK, Excel genera un reporte con toda la información
(ver tabla inferior). El reporte esta dividido en dos tablas, la primera
presenta el resumen descriptivo (numero de fincas, sumas, promedio y
varianza) para cada subregión por año, así como para la totalidad, y la
segunda tabla presenta el ANAVA para las subregiones (Sample), para los
años (Columns) y para la interacción de las dos variables.
Reporte generado por Excel listo para su interpretación
Enfocandonos en los resultados del ANAVA, la primera fila (Sample)
muestra los resultados de las filas que para nuestro ejemplo serian las
subregiones. Para este caso el valor de F (8.27) es mayor que el F
crítico (2.71) y el P-value es inferior a 0.0001 (inferior al valor de 𝛼
= 0.05) por tanto no podemos aceptar la H0 y podemos confirmar
con un 95% de confianza que las medias del SCC logarítmico son diferentes
entre regiones. En la siguiente fila tenemos el análisis de las columnas,
en este caso el valor de F (0.89) es inferior al F crítico (2.71) y el P-Value
(0.44) es superior al 𝛼 por tanto no podemos rechazar la H0 y
podemos afirmar con 95% de confianza que las medias del conteo SCC logarítmico
no son diferentes a través de los años, por tanto las medidas sanitarias
que se tomaron no se han reflejado en una mejora en los valores de las células
somáticas de los hatos de cada una de las regiones. Finalmente la última
fila nos muestra el efecto de la interacción (Año x Región) donde al igual
que para los resultados por año tampoco hay un efecto significativo.
ANAVA de dos factores con replicación (factorial)
 Vet Análisis Datos
Vet Análisis Datos