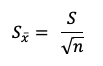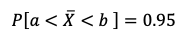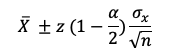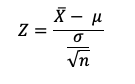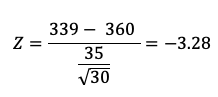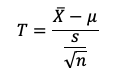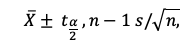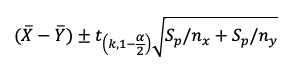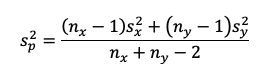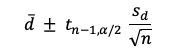6.3- Intervalos de confianza
El intervalo de confianza es un rango de valores que toma la variable en
el cual se tiene confianza con un determinado porcentaje (usualmente el
95%) que el parámetro poblacional se encuentre ubicado. El intervalo de
confianza es una representación mas certera de la realidad que solo dar
el valor de una media, especialmente cuando se trabaja con una muestra y
no con una población. El intervalo de confianza se debe construir
alrededor de un punto estimado.
Para obtener el intervalo de confianza de un parámetro por ejemplo estimar
la media, se van a determinar los números a y b de manera que:
Esto significa que con un 95% de confianza la media se encuentra entre
el punto a y el punto b. El nivel de confianza de un intervalo es una
probabilidad que representa la seguridad de que el intervalo encierra el
verdadero valor del parámetro que estamos buscando determinar. Para cada
nivel de confianza existe un valor de tabla (z, t, x2,F) asociado al nivel de confianza dado. Este es el coeficiente de confiabilidad.
El nivel de confianza se denota como 100(1 – 𝛼)%.
6.3.1- Intervalo con varianza poblacional conocida
Para este tipo de intervalo muestral debemos tener en cuenta
(greelane.com,2018):
-
- La muestra es pequeña en relación con la población. Normalmente el
tamaño de la población es veinte veces mayor que el tamaño de la
muestra.
- - La variable en estudio tiene una distribución normal.
- - Se conoce la desviación estándar de la población.
- - La muestra es aleatoria simple.
- - Se desconoce la media de la población.
Para este intervalo podemos fijar de antemano el grado de confianza de
que el verdadero valor de la media 𝛍x quede incluido en el rango. La
formula simplificada es:
Donde: z (1-α/2) = valor de la variable normal estándar que determina
una cola superior de medida 𝛂/2
Es importante recordar que el valor de confianza de 100(1 – 𝛼)% en la
tabla respectiva, debe buscarse un valor de variable para el cual el
área de la cola superior e inferior sea del 100(𝛼/2)%. Esto porque la
porción de área que no será cubierta por el intervalo se reparte en
partes iguales tanto en la cola superior como la inferior. Entonces si
es 5% las areas se repartirían 2.5% hacia la izquierda y 2.5% hacia la
derecha.
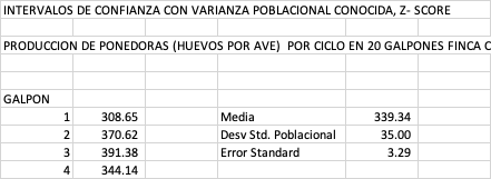
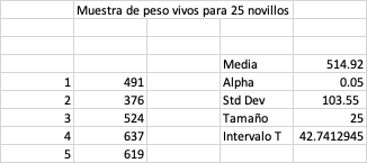
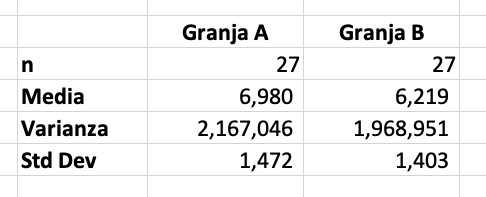
Ejemplo: en una granja avícola (huevos) en Santander Colombia, se hace un
muestreo aleatorio de las producciones de 30 lotes de ponedoras y se obtuvo
una media de 339 huevos por ave por por postura. El promedio de la producción
por ave por postura sigue una distribución normal y tiene una desviación
estándar 𝛔 = 35. El administrador de la finca no está de acuerdo con este
resultado ya que según sus cuentas, el promedio no puede bajar de 360 huevos
por ave por lote. Para determinar si lo que dice el administrador es cierto,
necesitamos comprobar si existe diferencia significativa entre la media encontrada
en el muestreo y la media suministrada por el administrador.
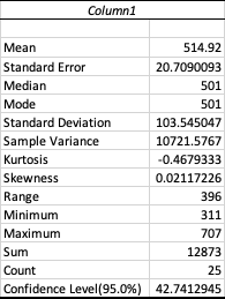
Entonces en Excel calculamos la media de las 30 muestras (=AVERAGE o =PROMEDIO) el dato de la desviación estándar, lo conocemos (35) y calculamos el error
estándar muestral. El error estándar nos permite estimar que tanto varia
la media muestral con respecto al valor de la que se obtendría calculando
la media poblacional. Se obtiene la siguiente manera:
Error Estándar Muestral = 35/√30 = 3.29
Donde 35 es el valor de la desviación estándar conocida y 30
corresponde la valor de muestras obtenidas.
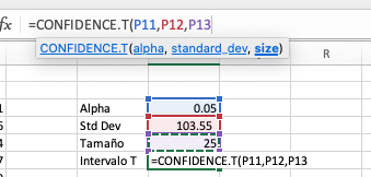
Para facilitar el manejo de la información podemos construir una pequeña
tabla en Excel tal como se muestra en la tabla inferior a la derecha.
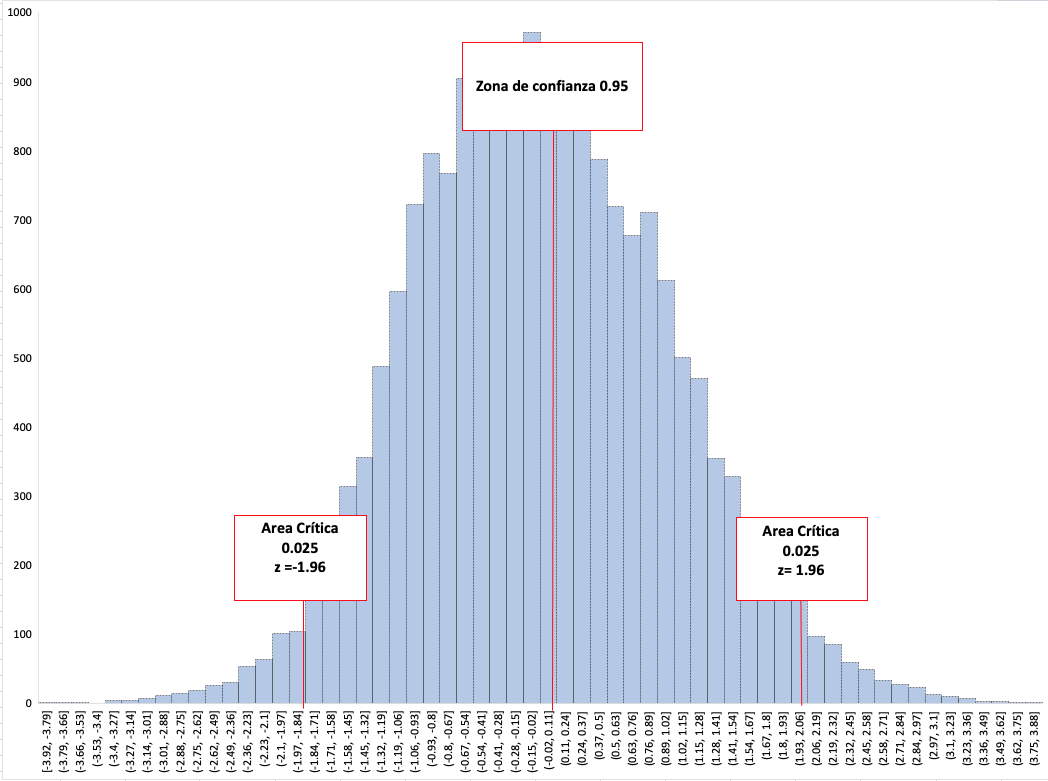
Entonces de la tabla z obtenemos el 𝛂/2, como queremos establecer un
intervalo de confianza del 95% entonces el 𝛂 seria 5/2 = 2.5% (la mitad
para cada cola). Este valor en la tabla es de 1.96. Entonces
reemplazamos en la formula para obtener el valor mínimo y el valor
máximo.
El valor para establecer el intervalo de confianza se puede
calcular en Excel por lo tanto no hay necesidad de tener una tabla. Para
ello utilizamos en inglés la función =NORM.S.INV o =DITR.NORM.ESTAND.INV en español. Esta función nos pide insertar el porcentaje de confianza en
este caso es del 95% pero hay que tener en cuenta que este se reparte entre
las dos colas, asi que el 𝛂/2 que en este caso es el 97.5% y el valor retornado
es igual al obtenido en la tabla o sea 1.96. Con este valor podemos construir
nuestro intervalo de confianza. Una vez tenemos el valor crítico de la tabla
podemos calcular el intervalo.
Valor mínimo = 339 – (3.29 * 1.96) = 332.55
Valor máximo = 339 + ( 3.29*1.96) = 347.82
Para calcular el intervalo en Excel, utilizamos la función =CONFIDENCE.NORM o =INTERVALO.CONFIANZA.NORM. Insertamos la función e incluimos el valor del 𝛂, la desviación
estándar y el tamaño de la muestra. Para este caso el valor es 12.52.
Entonces el intervalo será de 339 ± 12.52 con lo cual vamos a obtener
los mismos resultados calculados previamente. Entonces con un 95% de
confianza podemos decir que la media de producción por ave por lote en
esta finca es un valor que se encuentra entre 332.55 y 347.82 huevos por
ave por lote. Por tanto con un 95% de confianza podemos afirmar que la
media que el administrador estimó en 360 huevos por ave por lote, no es
acertada.
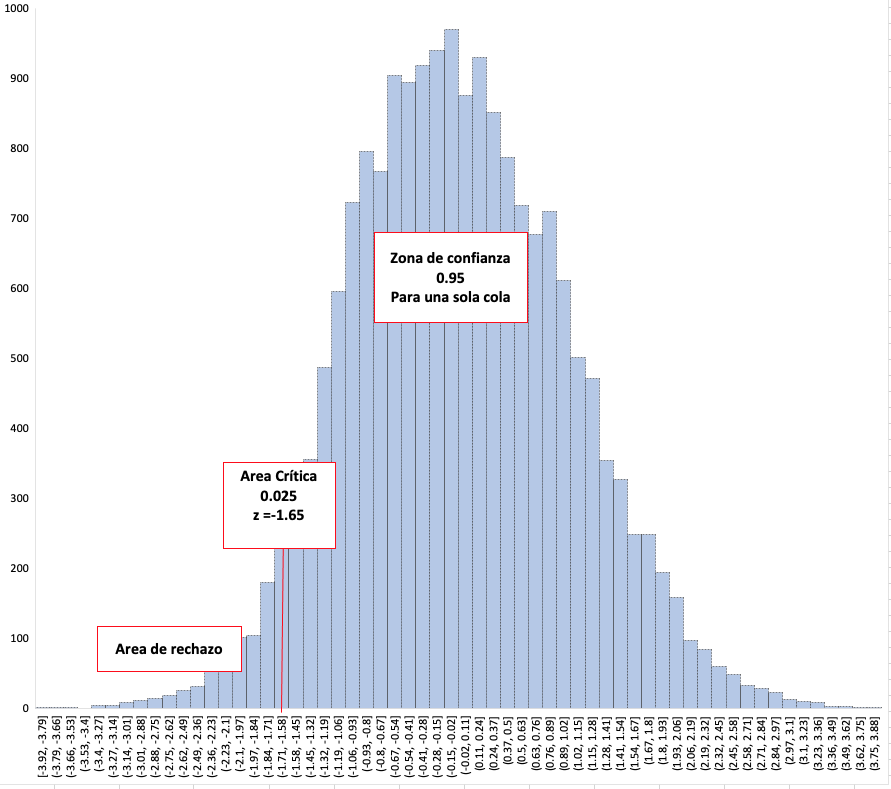
Vamos a ver otra manera de comprobar si el promedio es 360 huevos por
ave/encasetada como dice el administrador, para ello establezcamos las
hipótesis H0 y H1 donde:
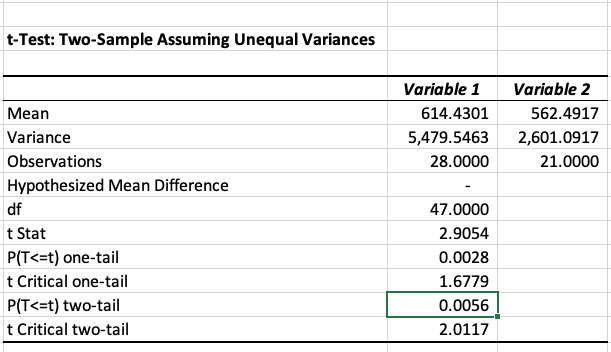
Como la hipótesis es una igualdad y una desigualdad entonces hablamos de
un ensayo de dos colas. Para demostrar si estas medias son iguales,
utilizamos la siguiente fórmula:
Donde X es la media muestral, 𝛍 es la media poblacional, σ
es la desviación estándar de la población y n el tamaño de la muestra.
Entonces, reemplazando:
El z calculado para una media de 360 es de -3.28 desviaciones estandar. El intervalo de z establecido para el 95% de confianza es entre -1.96 y 1.96 desviaciones estandar, por tanto -3.28 se encuentra por fuera de este rango y podemos decir con 95% de confianza que la media no es 360 huevos por ave por lote. Tal como lo habíamos previsto en nuestro intervalo de confianza.
Intervalo de confianza con varianza poblacional conocida
 Vet Análisis Datos
Vet Análisis Datos